Binomial Test and Binomial Value Calculators

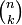
Compute the value of a binomial coefficient , given the value of the first nonnegative integer n, and the value of second nonnegative integer k. Knowing the value of a binomial coefficient can be very useful for analytics studies that incorporate combinatorics or the binomial distribution.

Compute the cumulative distribution function (CDF) for the binomial distribution, given the number of trials, the number of successes, and the probability of observing a successful outcome. The binomial distribution CDF is very useful for assessing probabilities in analytics studies that rely on the binomial experiments.

Compute the probability mass function (PMF) for the binomial distribution, given the number of trials, the number of successes, and the probability of observing a successful outcome. The binomial distribution PMF identifies the likelihood that an associated discrete random variable will have an exact value, and is very useful for analytics studies that rely on binomial experiments and probabilities.

Compute a binomial probability (that is, the probability of an individual binomial outcome), given the number of trials, the number of observed successes, and the probability of a successful outcome occurring. Knowing how likely it is that an individual binomial outcome will occur is very useful for analytics studies that involve binomial experiments.

Compute the 90%, 95%, and 99% confidence intervals for a binomial probability using the Clopper-Pearson (exact) method, given the total number of trials and the number of successes. Knowing the confidence interval for a binomial probability can be very useful for analytics studies that rely on binomial experiments.

Compute the expected value for a binomial random variable, given the number of trials and the probability of a successful outcome occurring. Knowing the expected value for a binomial variable is often very useful in analytics studies that rely on binomial experiments.

Compute the variance for a binomial random variable, given the number of trials and the probability of a successful outcome occurring. Knowing the variance for a binomial variable is often very useful in analytics studies that rely on binomial experiments.

Compute cumulative binomial probabilities (that is, the cumulative probability associated with a binomial outcome), given the number of trials, the number of observed successes, and the probability of a successful outcome occurring. The calculator will compute P(X<x), P(X≤x), P(X>x), and P(X≥x). Knowing the cumulative probability associated with a binomial outcome can be very useful for analytics studies that involve binomial experiments.